



以数织图也被称为Nonogram、Paint by Numbers或Griddlers,是一款流行的逻辑解谜游戏。这款游戏通过数字提示来填充网格中的方格,最终揭示出隐藏的图案。以数织图是一款充满挑战性的逻辑解谜游戏,适合喜欢动脑筋和解谜的玩家,快来下载试一试吧。
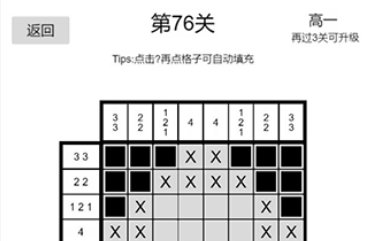
以数织图是一款用数字,织图画的休闲益智且烧脑的单机游戏,是一款非常考验玩家思维逻辑能力的佳作,玩法起源于起源于日本,以猜谜的方式绘画位图。在一个网格中,每一行和列都有一组数,玩家需根据它们来填满或留空格子,最后就可以由此得出一幅图画。游戏拥有挑战模式、对抗模式,模式中带有计时功能,这样更具有趣味性和挑战性,可玩性会更高,玩家可以在等公交或者听书无聊时玩一玩,消磨时间,感兴趣的朋友快来下载吧。
1、纵横数字和文字游戏都很好用,你很熟悉,游戏玩法很上瘾
3、5种挑战模式,选择最适合您的数织游戏难度等级
术语及定义:
排(行/列):指游戏中的水平或垂直排列。
垂直方向:与排的方向成90度角的方向。
m×n区块:表示一个矩形区域,其中m代表行数,n代表列数。未特指时,默认为整个游戏的所有排组成的集合。
场地格:游戏开始时存在的空格,是构成游戏区块的基本单位。
第x行格:从任意一边起始计数的第x个场地格。
第x个数字:从任意一边起始计数的第x个出现的数字。
数字x的正格:必须包含黑块的格子,并且这些格子属于数字x所代表的图形的一部分。
负格:确定不会包含黑块的格子。
数字x的位:数字x可能占据的场地格范围。
第一章:数字位置及其确定化
1-1 概述
在解数织谜题的过程中,玩家通过逻辑推理来确定模糊位置的确切坐标。利用场地格之间的关系以及已知信息,逐步缩小未知区域直至完成整幅图案。本章节旨在帮助初学者快速掌握推理技巧,成为能够解决大多数谜题的高手。
注释:在所有定理与方法讨论中,将负数视为零处理。
1-2 推演基础
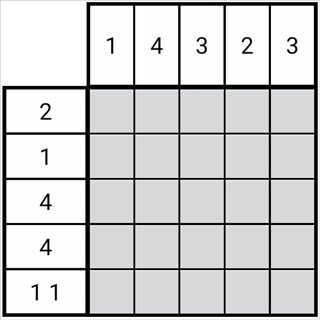
定理 1-2-1:如果一排只有一个数字,则该数字之外的场地格均为负格。
此定理表明,当一排仅有一个数字时,可以迅速确定非该数字所在位置的所有格子都为空白。
定理 1-2-2:若一排有且仅有一个数字k,并且已知第m行与第n行格为正格(m≥n),则从第(m-k+1)行到第(n+k-1)行之间的所有格都是该数字的正格。
这意味着,一旦确定了两个正格的位置,那么这两个正格之间以及向外扩展至数字k长度范围内的格子也必定是正格。
1-3 边缘法
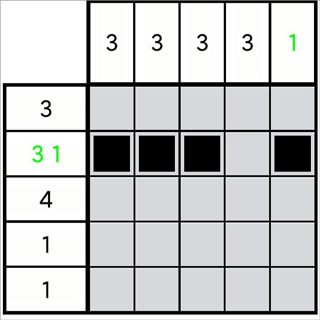
除了数字本身对位置的限制外,场地边缘同样能提供重要的定位线索。尤其是最接近边缘的数字,它们的位置更容易受到限制。
定理 1-3-1:若一排有且仅有一个数字m,并且已知第n行格为正格(m>n),则从第n行到第m行的格子都是正格。
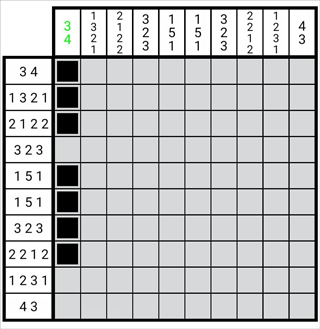
定理 1-3-2:若一排第一个数字为m,并且已知第n行格为正格(m>n),则从第n行到第m行的格子都是正格。
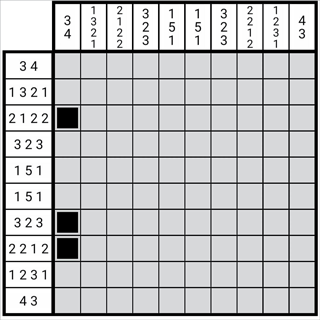
边缘状态下的推导方法可以帮助玩家更有效地确定正格的位置,尤其是在面对多数字组合的情况时。通过构造并调整边缘状态图形,玩家可以快速识别出潜在的正格,从而加快解题过程。
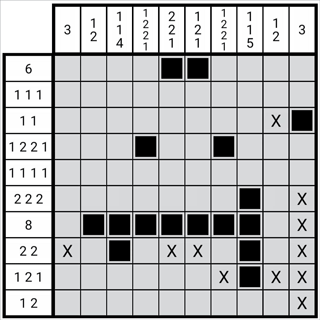
1、利用像素化逻辑谜题中来找到更多的线索,揭开其中隐藏的图像
2、纵横数字、文字游戏容易上手,是你熟悉的知识,玩法很上瘾
3、选择最适合自己的难度,从零开始逐渐来升级游戏中的难度